

Before I can explain my decades-long quest to map the starmaze I must acquaint you with a small puzzle. You will see a simple pattern consisting of nine cells. Each cell holds a shape - either a circle or a square. Each shape is either empty or filled.
Begin by clicking on the square in the center. The pattern will change. Keep clicking. Notice that the pattern will only change if you click on a filled shape. If you find yourself in a pattern with nine empty circles you will have reached a dead-end; click the "Start Over" button to return to the starting pattern.
To begin, see if you can predict how the pattern will change when you click a cell. Pay special attention to which patterns are filled and which are empty. Does it matter if a cell is in a corner, or on an edge, or in the center? Play for awhile.
Good. Now, go back to the start (reload this page) and see if you can figure out how to move from the starting pattern to the ending pattern (an empty circle surrounded by eight filled squares). Is that even possible? If so, how many moves are required? Please spend some time with the puzzle before continuing.
Pro tip: if you drag any pattern to the left, you can see a mystical description of its corresponding "room".
I first encountered this puzzle in the late 70s. It was not in the form you see it now. It consisted of asterisks (stars) arranged in a three-by-three numbered grid. The goal was to move from the pattern with only one star in the center to the pattern with stars in every cell but the center. I soon found the solution path, but then became intrigued. I had found the solution, but I didn't really understand it.
There was something deeply simple about this puzzle, and yet I couldn't quite grasp it. The solution path was mostly symmetrical (the last three steps were a mirror image of the first three) but something strange happened in the middle. Was it random or was I just failing to grasp the underlying principle? I was like a medieval astronomer trying to understand the movement of the planets.
I have a habit of seeing everything (cities, organizations, computers, networks, brains) as a maze, so I named this puzzle the starmaze. To see this puzzle as a maze, just imagine that each pattern corresponds to a separate room. The empty shapes in each pattern represent closed doors. The solid shapes represent open doors that lead (through dark twisty passages) to other rooms.
Given this insight, all I had to do was map the maze. I got out a piece of paper and began.
The first problem I ran into was that there were a lot of rooms, 512 to be precise. Even worse, there were a total of 2304 one-way passages. Even if I could find a big enough piece of paper, the thousands of little arrows would create an impenetrable mess.
My next approach was ingenious. The human mind, I reasoned, has evolved to understand exactly this type of spatial relationship. When you move to a new city, everything seems strange at first. But as you wander around things become more familiar. Without even trying you soon assemble a mental map of the city streets and even the insides of many different buildings. So all I had to do was build a city in the shape of the starmaze and wander around in it for awhile.
I invented wacky names for each room and then wrote a simple computer
program that let me move quickly from room to room (much as we now move from page
to page on the web). I then spent some time just wandering around and waited
for my mental map to emerge.
But something funny happened. No matter how I wrote and re-wrote the room
descriptions, they kept connecting in ways that just didn't make sense. I had
closet doors that opened into treehouses, tramways inside submarines, and
trap doors in the floor that led straight to the roof. And every room was about
the same distance from every other room. It wasn't like any space I'd ever
wandered through, and so my mental map never emerged.
Undaunted, I began using my computer like a telescope, writing programs to examine
the puzzle's mathematical structure (a practice I continue to this day). The more
I looked, the more mysterious things became. For example, I noticed that I could
paint half the rooms in the starmaze white, and the other half black, in such a way that
no matter how I moved, a white room would always lead to a black, and a black to a white.
There were no exceptions. I called these sun patterns and moon patterns. But what
did this mean?
Next, I wrote a program to find the shortest path from each room back to itself. When the
printout came out of the printer I couldn't believe it. The answer was the same for every
room: four. There were only four excecptions: the pit (the room with nine empty shapes from
which there is no escape), the source (the room with nine solid shapes to which you can never
return), the starting room, and the ending room (which both required six steps). By now
I had already begun to notice the "fourness" of the maze, the tendency to go round and
round in four step cycles. This had to mean something.
I began building models of maze sub-structures out of tinkertoys and colored yarn and hung
one of these over my desk as a mobile. One day I was daydreaming at my desk, thinking about
the maze, and lazily watching shadows dance on the wall as the mobile turned in the sun.
Diamond shapes grew and shrank, melting into each other. Suddenly it was as if the heavens
opened up and, for the briefest instant, everything was clear. The simplicity I had sensed
from the beginning was shining before me in a radiant light.
In that instant I finally grasped that the starmaze was arranged on the edges of a nine-dimensional
hypercube. This may sound complicated to those of you used to living in three-dimensional space,
but in fact it couldn't be much simpler. Like a cube, a hypercube is built entirely out of ordinary
squares. It's like a crystal, dazzling because of its perfect symmetry.
It also explained the fourness. Because no matter how many dimensions it lives in, a hypercube
is built out of 90 degree angles, and it always takes four 90 degree angles to come full circle (or
should I say "full square"). It also meant that a map was definitely possible.
The Hunt
Although I knew with certainty that a map was possible the instant I glimpsed the hypercube, I
also knew that it wouldn't be easy. In fact, it took me four years to finally draw the map. The
enormous simplicity of a cube makes it possible to organize the map into a manageable form. But
the sheer size of this cube, with its 2303 edges, makes the task, well, tricky.
All those edges created two problems. First, there were just too many of them. Second, the fact
that they were directed edges (one-way passages) meant lots of little arrows which make any diagram
harder to read. Some time after my initial insight I came across a clever idea that I thought might
be of some help.
This idea came, appropriately enough, from a fellow maze afficiando, Adrian Fisher, a maze designer
based in England. Mr. Fisher devised something he called color mazes, deceptively simple diagrams which
pack big mazes into small spaces by using colored passageways and rules which restrict movement.
In a two-color maze, for example, the rule might be that if you enter a room through a red passage,
you must leave it through a blue passage, and vice versa. In this way, a single room really represents
two distinct rooms, one which can be reached through a red passage, and another reached through a
blue passage.
I immediately realized that Fisher had found a way of drawing one-way passages without using arrows.
I felt certain that there must be some way of overlaying rooms in the starmaze to achieve this effect.
Because of the many symmetries in the hypercube, I thought it should be possible to divide the maze into two
mirror images which could then be folded back and overlaid one atop the other.
I eventually uncovered a method of doing just this by pairing each room with its inverse. Not only
did this eliminate the pesky arrows, it reduced the total number of rooms in the map by half!
Once I had mastered this technique, the next step was to use symmetry to break the remaining eight
dimensions into sixteen smaller four-dimensional mazes which could then be arranged in a simple
four-by-four grid. This is possible because an 8-cube can be understood as a 4-cube (tesseract)
in which each corner is itself a tesseract. It is relatively easy to draw the map of a tesseract,
since it has only 16 rooms and 32 passages. As I burrowed into this problem, I developed my
own private language, with terms like yin cells and yang cells.
The overall structure of the map was now clear to me. By holding the center and yin (corner) cells
constant and allowing only the remaining four yang cells to vary, I would create a tesseract of 16
rooms. These rooms would be arranged in a four-by-four grid and linked by colored pipes that created
a one-way flow from all yang cells solid to all yang cells empty. I called this mini-map a microcosm.
Once I had one microcosm defined, I could create another by flipping a single yin cell. Flipping
through all 16 combinations of yin cells created a total of 16 microcosms. I would then arrange
these 16 microcosms in the same sort of four-by-four grid and connect them with "macropipes". Each
macropipe would represent or contain the 16 pipes leading from a room in one microcosm to the
corresponding room in another microcosm. In practice I had to divide each macropipe into four pipes,
but this still reduced the total number of pipes in the map by a factor of four.
To finish, all that was needed was a series of "center-pipes". Each center-pipe would contain
pipes representing the change that takes place when a player clicks the center cell of a pattern.
Again, each center-pipe contained 16 smaller pipes and because of way the microcosms were defined,
only one center-pipe was needed to connect each pair of center-related microcosms. After much
experimentation, I discovered that I could further reduce the visual clutter by tilting each microcosm
45 degrees.
That was the theory, but in practice it was very hard to build each microcosm and wire them all together
so that everything worked. One stumbling block was the orientation problem. At first I thought I
could draw each room so that the northwest cell went out the northwest pipe, the north cell went out
the north pipe, etc. But I soon discovered that this is impossible.
To see why, just try deforming a map of the earth so that it is stretched across the six faces of
a cube. If you look at any of the six faces, it seems simple to draw in the points of a compass.
But if you follow the north arrow off one face and cross over to an adjoining face a strange thing
will happen. Instead of moving north you are now moving east. Or west. Or south! No matter how
you rearrange your compasses, there is no way to get them all to connect together in a consistent
way. Try it yourself.
For the starmap, this added a subtle complication. In one room, the northwest cell might feed
into the northwest pipe. But in a nearby room, the northwest cell might feed into the southeast
pipe. I could correct for this by adding more pipes winding around each room, but that would have
greatly increased the complexity and size of the map. Instead I just defined a compass orientation
for each room. It turned out that there were 16 different orientations in the starmaze, and now I
had to create and keep track of a meta-map which described which rooms used which orientations.
What made it worse was that nothing was fixed. I could connect the 16 rooms of a microcosm in a myriad
of different ways, and each way would require a different meta-map of orientations. Every time I
fixed one problem, another would spring up somewhere else. I would adjust the orientations, and then
all the pipe layouts had to be changed (and re-colored). But when I adjusted the pipe layouts, the
orientations had to be changed. For years I filled blackboards late at night without finding the
right balance.
It was about this time when I had the opportunity to become a caretaker and retreat to a remote cottage
high in the Montana Rockies. I had just upgraded my trusty Macintosh computer to the latest model (an SE with
an astonishing ONE megabyte of memory) and a pre-release version of a strange new program called Hypercard
which looked like it could help me quickly visualize complex structures. So I decided to focus completely
on this problem and solve it once and for all. It took three months of almost uninterrupted work, but I
finally did it.
Finding the final solution was a mystical experience. I got into such a complete state of
concentration that I could feel my way through the problem. I gave up trying to calculate the solution
in a logical way and instead just closed my eyes and reached for certain layouts. I used the computer
to check each attempt. When something failed I got so I could almost feel where the problem was.
Finally I gave all the pipes a peculiar twist, ran my program, and instead of beeping at me it
gently glided to a halt and said nothing at all. I had found it!
The Map
There was no such thing as a color printer in 1987 (at least in my price range), and so to actually create
the map I had to print out 16 intricately designed sheets, tape them together, and color in each microscopic
room and pipe by hand. Which I did.
Following are the actual diagrams and maps I created. Click each
thumbnail to view a full-size version.
 Now everything made sense. The reason my mental map never emerged was that I had been wandering
in a nine-dimensional space. In two dimensions, or even three, it was a tangled mess, but in nine
dimensions it was just a big square. This is why there was no near and far, why all the rooms were
more or less the same distance apart. It explained the day-and-nightness, though this was not
immediately obvious. (It has to do with the fact that every corner of a hypercube has a binary
address with an odd or even number of 1s and 0s which flip one at a time as you traverse the edges.)
Now everything made sense. The reason my mental map never emerged was that I had been wandering
in a nine-dimensional space. In two dimensions, or even three, it was a tangled mess, but in nine
dimensions it was just a big square. This is why there was no near and far, why all the rooms were
more or less the same distance apart. It explained the day-and-nightness, though this was not
immediately obvious. (It has to do with the fact that every corner of a hypercube has a binary
address with an odd or even number of 1s and 0s which flip one at a time as you traverse the edges.)
 |
Here is a photograph of the actual star map which still hangs on my wall. It took days to color in the thousands of interwoven pipe segments with blue and red marking pens. |
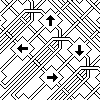 |
Here is the diagram I used to determine the structure and orientation of the original map. It serves as the blueprint from which the map was constructed. |
 |
This diagram determines how the pipes in the maze are colored. The colors are what gives the maze its one-way movement. |
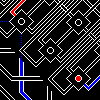 |
Here is a poster which shows the solution path. For more details on how to follow a path room by room using the map, see Reading the Solution. |
Beyond The Map
The starmap marked the end of one phase in my exploration, and the beginning of another. Once I understood how the rooms in the maze were arranged, it became possible to search for endless new patterns and visualize them by simply plotting them on the map. What was chaos suddenly became cosmos. The map made it possible for me to find my bearings and confidently set out on one journey after another.
The first thing I did was to create a program on the computer (a HyperCard stack) which recreated the map in software form. This made it possible to move from room to room with a blinking cursor showing my current position, plot subsets of rooms to reveal hidden patterns, calculate paths, and keep a kind of lab notebook of all my findings. Remarkably, the entire map, in abstract form, now fit easily even on the small screens of the time.
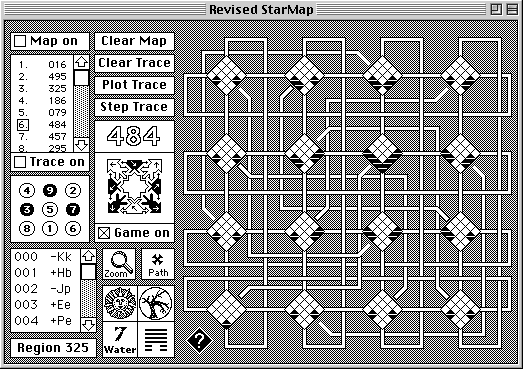
The above screenshot shows a typical plot of all 96 of the rooms involved in the 1920 possible solutions to the eleven-step puzzle posed at the top of this page. The rooms are plotted against a revised version of the starmap I completed in 1998. For more information about this remarkable program, see The Starmaze Explorer.
 With the Starmaze Explorer as my telescope I spent many sleepless nights scanning the starmaze heavens
for new discoveries. The patterns in the maze acquired forms,
elements, and seasons.
I inscribed hexagrams over the entrance to every passage.
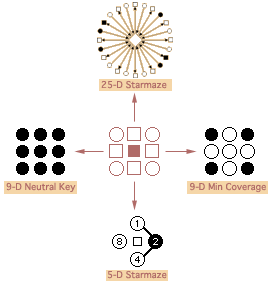
I established a larger context for the starmaze by studying other dimensions
of the maze from a 5-D starmaze to a 25-D starmaze and beyond. And when I realized that the starmaze
was just one example of a larger class of hypercube puzzles, I broadened that context even further
by studying a whole range of variations, from "Neutral Key" puzzles to "Minimum Coverage" puzzles and many others in between.
With the Starmaze Explorer as my telescope I spent many sleepless nights scanning the starmaze heavens
for new discoveries. The patterns in the maze acquired forms,
elements, and seasons.
I inscribed hexagrams over the entrance to every passage.
I established a larger context for the starmaze by studying other dimensions
of the maze from a 5-D starmaze to a 25-D starmaze and beyond. And when I realized that the starmaze
was just one example of a larger class of hypercube puzzles, I broadened that context even further
by studying a whole range of variations, from "Neutral Key" puzzles to "Minimum Coverage" puzzles and many others in between.
Each one of these investigations was like staring into a different facet of a sparkling jewel. My purpose was always to find a deeper understanding. Whenever I discovered a new property of the maze, I asked "why?" If there was a superficial answer to that question I asked "why?" again, and kept asking in a very child-like way until I was satisfied.
My latest project is the realization of a fully 3D version of the starmaze. Using a 3D modeling program I am "excavating" a vast monastery of towers and courtyards and underground caverns. My ultimate goal is to create a memory palace so vivid that I can calculate shortest paths by just seeing the answer. For more information about this project, see starmaze 3D.
In the decades which have transpired since I first laid eyes on the map, my fascination with the starmaze has only increased. I continue to uncover remarkable new properties, and new challenges. The maze has become not just a bizarre hobby, but a kind of movable feast, a quiet world I can retreat into at any time for peaceful contemplation. So far I am the sole occupant of the maze, but I hope these web pages will allow others to share some of my discoveries.
NOTE: Unlike the other exhibits in the Museum of Play Maps, the starmaze is still active. So I fully expect to add new pages and revise existing ones. Starmaze designs and content are copyright John Cartan, all rights reserved.